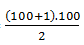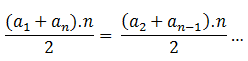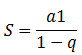Progressão Aritmética e PG

Bom, pessoal, aqui vai um resumo do que é basicamente o assunto Progressão Aritmética e Geométrica junto com algumas demonstrações, para que não seja preciso ficar decorando as fórmulas, mas saber como chegar nelas. Os exercícios no final estão sem resposta, mas podem ser tiradas dúvidas no grupo pelo facebook.

Progressão Aritmética

                Podemos entender por progressão aritmética uma sequência numérica na qual, dentro dela, haja uma razão definida por uma adição ou subtração do primeiro termo. Por exemplo:

(a₁, a₂, a₃, ..., a_n)

Na sequência acima temos os termos da P.A. (a₁, a₂, a₃, ..., a_n) e, como citado anteriormente, tem de haver uma razão, de modo que:

r = a₂ – a₁ = a₄ – a₃ = a_n – a_n-1

                Para esclarecermos as definições de cada coisa em uma P.A., vamos usar valores numéricos, como:

(1, 2, 3, 4, 5, ..., 100)

Nessa sequência temos os termos: 1, 2, 3, 4, 5, ..., 100.
E, consequentemente, uma razão: r = 2 – 1 = 3 – 2 = 4 – 3 = 100 – 99 = 1.

Conhecendo a razão e os termos, vemos que:

a₂ = a₁ + 1.r

a₃ = a₁ + 2.r

a₄ = a₁ + 3.r

a_n = a₁ + (n-1).r

Ou ainda:

a_n = a_k + (n-k).r

Se quisermos saber o 27º número da sequência, basta usarmos a relação descoberta anteriormente:

a_{27 =} 1 + (27-1).1 = 27 

Para podermos somar todos os números que compõem a P.A., há uma relação descoberta por Gauss da seguinte maneira:

A soma dos 100 termos da P.A. é:

S = 1 + 2 + 3 + 4 + 5 + 6 + ... + 99 + 100

Sabe-se, ainda, que a ordem não altera o resultado da soma, logo:

S = 100 + 99 + ... + 6 + 5 + 4 + 3 + 2 + 1

Somando as duas:

S + S = 100 + 1 + 99 + 2 + ... + 99 + 2 + 100 + 1

2S = 101 + 101 + 101 + ... + 101 (100 vezes)

2S = 101.100

S= 

Com isso, Gauss viu que, numa P.A. de n termos, a soma pode ser efetuada por:

Ou ainda:

S=

Numa P.A. de n termos, em que n é um número ímpar, podemos ver que em:

(a₁, a₂, a₃, a₄, a₅)

a₃ é o termo central. Tomando relação entre progressões aritméticas diferentes:

I-                    (1, 3, 5, 7, 9)

II-                  (2, 6, 10, 14, 18, 22, 26 )

III-                (10, 13, 16, 19, 22, 25, 28)

Vimos que o termo central é a média aritmética entre o primeiro e o último termo. Então a soma de uma P.A. também pode ser feita:

S = T_c . n, em que T_c é o termo central.

I-                    S = 5 . 5 = 25

II-                  S = 14 . 7 = 98

III-                S = 19 . 7 = 133

Exercícios

1)     (Projeto Nerd)Uma progressão aritmética tem razão igual a 3 e 1º termo igual a 1. Determine:

a)      o 13º termo;

b)      a soma dos 60 primeiros termos;

2)     (Projeto Nerd)Em uma P.A. de 13 termos e razão 2, a₇ = 14. Pede-se:

a)      a soma de todos os termos dessa progressão;

b)      o primeiro e o último termo;

3)    (Projeto Nerd)  Dada a P.A. (3x+y,  x+6y,  2x+3y), a relação x/y é igual a

a)      -3/8                       b) -8/3                  c)3/8                     d)8/3

4)     (Projeto Nerd)Considere uma determinada arma com uma capacidade infinita de munição e capaz de atirar 2 balas por segundo se seu gatilho for apertado pausadamente. E, quando


apertado continuamente, são disparadas balas de forma que a quantidade de balas disparadas a cada segundo formem uma P.A. de razão r = 1. Sabendo que a arma dispara 2 balas no primeiro segundo, se o gatilho permanecer apertado por um minuto, quantas balas serão disparadas?

a)      945                        b) 1890                 c) 3780                 d)nda

5)     (Projeto Nerd)Sabe-se que o terceiro termo de um P.A. com 10 termos é 4 e o antepenúltimo termo é 19. Determine a soma dessa sequência.


6)  (Projeto Nerd) Um triângulo retângulo de área 1200ua tem seus lados em progressão aritmética. Mostre-os.

Progressão Geométrica

                Assim como a progressão aritmética, a geométrica é uma sequência de números que têm relação entre si, que é a razão (q). A sequência:

(a₁, a₂, a₃, ..., a_n)

só será uma P.G. se:

                Por exemplo:

I-                    (1, 3, 9, 27, 81, ...), em que q = 3

II-                  (20, 10, 5), em que q = ½

III-                (2, -4, 8, -16, 32), em que q = -2

Na primeira, temos que:

3 = 1 . q

9 = 1 . q . q

27 = 1 . q . q . q

Então o quarto termo será a₄ = a₁ . q^4-1

Ou ainda:

a_n = a_k . q^n-k

Se quisermos saber o 5º termo dessa P.G., basta usarmos essa relação.
a₆ = 1. 3^6-1 = 243

Também podemos determinas a soma dos termos de uma P.G. da seguinte maneira:

Temos que a soma é

S = a₁ + a₂ + ... + a_n e também

S = a₁ + a₁.q + a₁.q² + ... + a₁.q^n-1 (I), multiplicando por q

q.S = a₁.q + a₁.q² + ... + a₁.qⁿ (II), fazendo (II) – (I)
qS – S = a₁.qⁿ – a₁ <-> S.(q – 1) = a_1.(qⁿ – 1)

e chegamos em 

Se precisarmos somar os termos da P.G. (20, 10, 5), basta fazer

Mas numa P.G, também é possível determinar sua soma se ela for infinita e satisfaça a condição  |q| < 1. Veja como é possível:

Se a₁ = 1 e q = ½, chegará um termo em que seu valor será muito próximo de zero e, portanto, desprezível. Por exemplo:

a₁₀ = 1. (½)¹⁰ = 0,00097

Se considerarmos o termo a_n = a₁.qⁿ = 0, chegamos em:

(20, 10, 5, ...) tem soma igual a

S = 40

Exercícios

1)      (Projeto Nerd) Seja a sequência (2, 4, 8, 16, ...) uma PG, determine:

a)      seu 14º termo;

b)      a soma dos 10 primeiros termos.

2)      (Projeto Nerd) Determine os valores dos termos da PG (x+2, 4x+1, 12x+3) com q ≠ 0.

3)      (Projeto Nerd) Determine a soma de (1,2,3,4,5,8,7,16,...17, 512).

4)       Qual a soma da PG infinita (1, 1024, 512, 256, ...) ?

Victor R.